MOMEN INERSIA
Momen inersia (Satuan SI : kg m2) adalah ukuran kelembaman suatu benda untuk berotasi terhadap porosnya. Besaran ini adalah analog rotasi dari pada massa. Momen inersia berperan dalam dinamika rotasi seperti massa dalam dinamika dasar, dan menentukan hubungan antara momentum sudut dan kecepatan sudut, momen gaya dan percepatan sudut, dan beberapa besaran lain. Meskipun pembahasan skalar terhadap momen inersia, pembahasan menggunakan pendekatan tensor memungkinkan analisis sistem yang lebih rumit seperti gerakan giroskopik.
Lambang dan kadang-kadang juga
dan kadang-kadang juga  biasanya digunakan untuk merujuk kepada momen inersia.
biasanya digunakan untuk merujuk kepada momen inersia.
Konsep ini diperkenalkan oleh Euler dalam bukunya a Theoria motus corporum solidorum seu rigidorum pada tahun 1730.
Lambang
 dan kadang-kadang juga
dan kadang-kadang juga  biasanya digunakan untuk merujuk kepada momen inersia.
biasanya digunakan untuk merujuk kepada momen inersia.Konsep ini diperkenalkan oleh Euler dalam bukunya a Theoria motus corporum solidorum seu rigidorum pada tahun 1730.
Momen inersiapartikel bisa ditulis dalam persamaan atau rumus matematika I = mr2
I= momen inersia(satuan kgm2)
m = massa (satuan kg)
r =jarak partikel ke sumbu putar (satuan m).
Jika terdapat banyak partikel atau lebih dari satu dengan massa mi dan jaraknya ri terhadap poros atau sumbu putar maka momen inersia total adalah jumlah aljabar dari masing-masing momen inersiapartikel tau ditulis dalam bentuk persamaan berikut
Momen inersia benda yang berotasi dengan sumbu putar di titik tertentu dinyatakan dengan persamaan
Teorema Sumbu Sejajar
Keterangan
I= momen inersia terhadap sembarang sumbu
Ipm= momen inersia terhadap pusat massa
M= massa total benda
a=jarak sumbu pusat massa ke sumbu paralel.
Persamaan diatas dikenal dengan Teorema sumbu sejajar atau teorema sumbu paralel
Teorema Sumbu sejajar digunakan untuk menghitung momen Inersia suatu bangun yang diputar dengan poros tidak pada pusat massa(pm) atau sembarang tempat. Bila momen inersia sebuah benda terhadap pusat massa(Ipm) diketahui, momen inersia terhadap sembarang sumbu yang sejajar(paralel) terhadap sumbu pusat massa dapat dihitung dengan persamaan
I= momen inersia terhadap sembarang sumbu
Ipm= momen inersia terhadap pusat massa
M= massa total benda
a=jarak sumbu pusat massa ke sumbu paralel.
Persamaan diatas dikenal dengan Teorema sumbu sejajar atau teorema sumbu paralel
contoh soal :
Soal No. 1
Susunan 3 buah massa titik seperti gambar berikut!

Jika m1 = 1 kg, m2 = 2 kg dan m3 = 3 kg, tentukan momen inersia sistem tersebut jika diputar menurut :
a) poros P
b) poros Q
Pembahasan
a) poros P

b) poros Q

Susunan 3 buah massa titik seperti gambar berikut!

Jika m1 = 1 kg, m2 = 2 kg dan m3 = 3 kg, tentukan momen inersia sistem tersebut jika diputar menurut :
a) poros P
b) poros Q
Pembahasan
a) poros P

b) poros Q

Soal No. 2
Bola A bermassa = 60 gram dan bola B = 40 gram dihubungkan batang AB (massanya diabaikan).

Jika kedua bola diputar dengan sumbu putar di P maka momen inersia sistem adalah….
A. 12,25 .10 –4 kg m2
B. 13,50 .10 –4 kg m2
C. 14,50 .10 –4 kg m2
D. 15,50 .10 –4 kg m2
E. 16,25 .10 –4 kg m2
(Momen Inersia - UN Fisika 2013)
Bola A bermassa = 60 gram dan bola B = 40 gram dihubungkan batang AB (massanya diabaikan).

Jika kedua bola diputar dengan sumbu putar di P maka momen inersia sistem adalah….
A. 12,25 .10 –4 kg m2
B. 13,50 .10 –4 kg m2
C. 14,50 .10 –4 kg m2
D. 15,50 .10 –4 kg m2
E. 16,25 .10 –4 kg m2
(Momen Inersia - UN Fisika 2013)
Pembahasan
Momen inersia di titik dengan sumbu putar di p

Soal No. 3
Lima titik massa tersusun seperti gambar berikut!

m1 = 1 kg, m2 = 2 kg , m3 = 3 kg, m4 = 4 kg, m5 = 5 kg
Tentukan momen inersianya jika:
a) poros putar sumbu X
b) poros putar sumbu Y
Pembahasan
a) poros putar sumbu X

b) poros putar sumbu Y

Soal No. 4
Tiga buah benda masing-masing :
Bola pejal massa 5 kg
Silinder pejal massa 2 kg
Batang tipis massa 0,12 kg
D = 2 m

Tentukan momen inersia masing- masing benda dengan pusat benda sebagai porosnya!
Pembahasan
Bola Pejal

Silinder Pejal
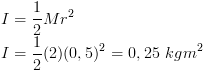
Batang Tipis

Momen inersia di titik dengan sumbu putar di p

Soal No. 3
Lima titik massa tersusun seperti gambar berikut!

m1 = 1 kg, m2 = 2 kg , m3 = 3 kg, m4 = 4 kg, m5 = 5 kg
Tentukan momen inersianya jika:
a) poros putar sumbu X
b) poros putar sumbu Y
Pembahasan
a) poros putar sumbu X

b) poros putar sumbu Y

Soal No. 4
Tiga buah benda masing-masing :
Bola pejal massa 5 kg
Silinder pejal massa 2 kg
Batang tipis massa 0,12 kg
D = 2 m

Tentukan momen inersia masing- masing benda dengan pusat benda sebagai porosnya!
Pembahasan
Bola Pejal

Silinder Pejal
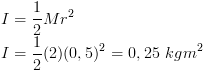
Batang Tipis

.jpg)
Komentar
Posting Komentar